Partielle Integration (Integralrechnung)
Die Partielle Integration wird auch Produktintegration genannt.
Damit ist es möglich zwei Funktionen zu integrieren, indem man von einer Funktion die Ableitung und von der anderen Funktion die Stammfunktion bildet.
Dieses Beispiel zeigt die Integration einer Polynomfunktion im Prdukt mit der e-Funktion. Hier wird die Polynomfunktion differenziert, da ab der zweiten Ableitung nur noch eine Konstante übrig bleibt. Die e-Funktion wird integriert, da die Stammfunktion dieselbe ist. Generell versucht man die einfachere der beiden Funktionen zu integrieren und die schwierigere Funktion zu differenzieren.

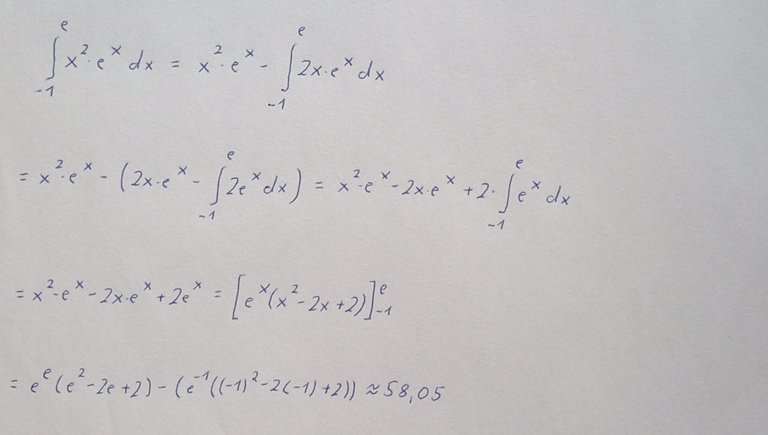
These photos were taken with my smartphone
0
0
0.000
Mir ist gerade eingefallen... was jetzt doof fuer dich ist^^, das Du vielleicht Beispiele mit dazu tun koenntest, was man dann damit in der Realwelt anfaengt. So einfach nur, damit die "Bandbreite" der Moeglichkeiten zum Lernen hoeher wird? Aber das ist nur mehr Arbeit fuer dich! Also nix worauf man einfach Eingehen sollte.^^
Ich glaube deine super sauberen Arbeiten, landen sowieso irgendwie dann da, wo sie hingeohren.
Ich mag wie diese Formel aussieht. Das ist so eine Hoffnungsformel. Die Hoffnung, das ich eines Tages die Kroete schlucke. Aber ich bin sicher, das Du stolz drauf sein kannst, das ich endlich das Geburtstagspardoxon im Schlaf erklaehren kann.^^ Das hat auch viel mit deinem Lehrmaterial zu tun. Du bist der Einziche, sacht der Franke, bei dem ich Mathe lerne, außerhalb der Coding Welt. :-)
Ich weis das ich irgendwann mal mit Integralrechnungen was gelesen habe. Deswegen auch die Verbindung zum "Realweltbeispiel" gefragt.
Liebe Grueße und beste Gesundheit dir und deinen Liebsten gewuenscht.
Sascha
Ein Beispiel wäre die Flächenberechnung zwischen zwei Funktionen.
Die Integralrechnung wird z.B. verwendet wenn man kurvige Flächen berechnen möchte. Also wenn man Flächen nicht so einfach berechnen kann wie ein Rechteck oder Kreis.
Die Produktintegration ist eine Möglichkeit solche Flächen zu bestimmen.
Dann weis ich jetzt auch woher ich das mal gesehen haben muss. Perfekt danke dir. :-)